Ensino Médio

1º ANO - ENSINNO MÉDIO

    o   Conjuntos numéricos;

  o   Números naturais, inteiros, racionais, irracionais e reais;

  o   Reta real;

  o   Estatísticas;

  o   Função;

  o   Gráficos de funções;

  o   Funções do 1º grau, crescente e decrescente;

  o   Gráfico cartesiano;

  o   Função do 2º grau;

  o   Inequação;

  o   Estudo de sinais

  o   Progressão aritmética ( PA );

  o   Progressão Geométrica ( PG );

  o   Relação entre duas grandezas;

  o   Proporção direta e indireta;

  o   Função do 1º grau;

  o   Função do 2º grau;

  o   Módulo de um número real;

  o   Função do módulo.

  o   Função exponencial;

  o   Equações exponenciais;

  o   Inequações exponenciais;

  o   Logaritmo;

  o   Equações logarítmicas;

  o   Mudança de base;

  o   Função logarítmica;

  o   Inequação logarítmica.

  o   Trigonometria;

  o   Triângulo retângulo;

  o   Teorema de Pitágoras;

  o   Teorema de Talles;

  o   Relação trigonométrica no triângulo retângulo;

  o   Cálculo do seno, cosseno e tangente;

  o   Tabelas trigonométricas;

  o   Noção de ângulos;

  o   Arco da circunferência;

  o   Ângulo central;

  o   Medidas de arco na circunferência;

  o   Círculo trigonométrico;

  o   Leis dos senos.

_________________________________________________________________________________

CONJUNTOS NUMÉRICOS

Conjunto dos Números Naturais
São todos os números inteiros positivos, incluindo o zero. É representado pela letra maiúscula N.
Caso queira representar o conjunto dos números naturais não-nulos (excluindo o zero), deve-se colocar um * ao lado do N:

N = {0,1,2,3,4,5,6,7,8,9,10, …}
N* = {1,2,3,4,5,6,7,8,9,10,11, …}

Conjunto dos Números Inteiros
São todos os números que pertencem ao conjunto dos Naturais mais os seus respectivos opostos (negativos).
São representados pela letra Z:

Z = {… -4, -3, -2, -1, 0, 1, 2, 3, 4, …}

O conjunto dos inteiros possui alguns subconjuntos, eles são:

- Inteiros não negativos
São todos os números inteiros que não são negativos. Logo percebemos que este conjunto é igual ao conjunto dos números naturais.
É representado por Z₊:

Z₊ = {0,1,2,3,4,5,6, …}

- Inteiros não positivos
São todos os números inteiros que não são positivos. É representado por Z_-:

Z_- = {…, -5, -4, -3, -2, -1, 0}

- Inteiros não negativos e não-nulos
É o conjunto Z₊ excluindo o zero. Representa-se esse subconjunto por Z*₊:

Z*₊ = {1, 2, 3, 4, 5, 6, 7, …}

Z*₊ = N*

- Inteiros não positivos e não nulos
São todos os números do conjunto Z_- excluindo o zero. Representa-se por Z*_-.

Z*_- = {… -4, -3, -2, -1}

Conjunto dos Números Racionais
Os números racionais é um conjunto que engloba os números inteiros (Z), números decimais finitos (por exemplo, 743,8432) e os números decimais infinitos periódicos (que repete uma sequência de algarismos da parte decimal infinitamente), como “12,050505…”, são também conhecidas como dízimas periódicas.
Os racionais são representados pela letra Q.

Conjunto dos Números Irracionais
É formado pelos números decimais infinitos não-periódicos. Um bom exemplo de número irracional é o número PI (resultado da divisão do perímetro de uma circunferência pelo seu diâmetro), que vale 3,14159265 …. Atualmente, supercomputadores já conseguiram calcular bilhões de casas decimais para o PI.
Também são irracionais todas as raízes não exatas, como a raiz quadrada de 2 (1,4142135 …)

Conjunto dos Números Reais
É formado por todos os conjuntos citados anteriormente (união do conjunto dos racionais com os irracionais).
Representado pela letra R.

_________________________________________________________________________________

RETA REAL

O conjunto dos números reais é formado a partir da união dos seguintes conjuntos:
Números Naturais: (0,1,2,3,4,5,6,7,8,9,....)
Números Inteiros: (....,-3,-2,-1,0,1,2,3,.....)
Números Racionais: (números na forma de a/b, com b≠0 e decimais periódicos. Ex:
1/2; 3/5; 0,25; 0,33333.....)
Números Irracionais: (números decimais não periódicos. Ex. 0,2354658752485879.....)

Intervalo Real

Intervalo aberto em a e aberto em b, ]a,b[ , {xЄR/a < x < b}
Aberto à esquerda e aberto à direita




Intervalo aberto em a e fechado em b, ]a,b], {xЄR/a < x ≤ b}
Aberto à esquerda e fechado à direita




Intervalo fechado em a e aberto em b, [a,b[, {xЄR/a ≤ x < b}
Fechado à esquerda e aberto à direita



Intervalo fechado em a e fechado em b, [a,b], {xЄR/a ≤ x ≤ b}
Fechado à esquerda e fechado à direita

Intervalos infinitos

{xЄR/x > a}

{xЄR/x

{xЄR/x≥a}



{xЄR/≤a}

_________________________________________________________________________________

ESTATÍSTICA

OBSERVE A SEGUINTE TABELA:

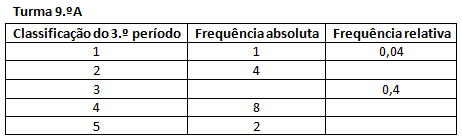
1. Complete a tabela.

2. Determine a porcentagem de alunos que tem positiva.

3. Indique a moda.

4. Determine a mediana.

5. Determine a classificação média.

 Resolução do exercício:

1.

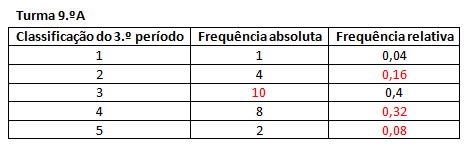
N.º total de alunos: 1+4+10+8+2=25

 2.

10+8+2=20

R.: 80%

3.

A moda é o valor mais frequente.
Logo, a moda é 3.

 4.

A mediana é o valor central ou a média aritmética dos valores centrais, depois de colocados os dados por ordem crescente.

1, 2, 2, 2, 2, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 4, 4, 4, 4, 4, 4, 4, 4, 5, 5.

Logo, a mediana é 3.

 5.

_________________________________________________________________________________

FUNÇÕES

Aplicações de uma Função Exponencial
Exemplos de aplicação de uma função exponencial.
Área sob uma Curva
Determinando a área de uma região através do cálculo da Integral.
Composição de três ou mais funções
Estudo das funções compostas.
Coordenadas de Localização Absoluta
Localização de pontos na esfera terrestre.
Fórmulas Fundamentais de Integração
Conheça as fórmulas para a integração de funções.
Função
Introdução ao estudo das funções.
Função Composta
Conheça a composição de uma função.
Função definida por fórmula
Leis de formação de funções.
Função Exponencial
Propriedades e características de uma função exponencial.
Função inversa
Determinando a função inversa.
Função Logarítmica
Estudo da Função Logarítmica.
Função modular
Definição e gráficos da função modular
Função Par e Função Ímpar
Saiba identificar uma função par ou ímpar.
Função Polinomial
Conheça a definição e as propriedades de uma função polinomial. Clique aqui!
Função quadrática na forma canônica
Determinando a forma canônica da função quadrática através da manipulação algébrica. Expressão canônica da função quadrática.
Funções e Matemática Financeira
Gráficos: juros simples e compostos.
Funções periódicas
Definição das funções periódicas e alguns exemplos. Compreendendo e definindo as funções periódicas e estudando o período de funções desse tipo.
Inequação modulares
Definição e propriedades de uma inequação modular.
Inequação Produto e Inequação Quociente
Estudo das Inequações.
Introdução à Função
Estudos introdutórios envolvendo função.
Limite de uma Função
Noção de Limite.
Matemática na Economia: Função Custo, Função Receita e Função Lucro
funções custo, receita e lucro.
Máximo e Mínimo da função na forma canônica
Analisando os coeficientes da função quadrática canônica para determinar os valores de máximo e mínimo. Obtendo os valores de máximo e mínimo de uma função quadrática.
Pontos de Nivelamento
Pontos críticos da função lucro.
Propriedades de uma função
Função, Característica de função, Função sobrejetora, Função injetora, Função bijetora, Imagem de uma função, imagem, imagem de uma função, contra domínio, Contra domínio de uma função.
Relação
Conceito de relação, Gráficos que representam uma relação, Gráfico que representa uma função, Domínio de uma relação, Imagem de uma relação, Forma de escrever uma relação, Par ordenado, Representação gráfica, Representação de uma relação através de uma re
Representação Gráfica de Funções
Funções e suas representações gráficas.
Taxa de Variação da Função do 2º Grau
Inclinação da reta tangente à parábola.
Tipos de Função
Propriedades e definição dos tipos de função.

Explicação de cada uma das funçõe em: 

http://www.brasilescola.com/matematica/funcoes.htm

________________________________________________________________________

PRINCIPAIS GRÁFICOS DE FUNÇÕES:

Sob um ponto de vista operacional, uma função pode ser considerada um conjunto de pares ordenados (x; y), criados de acordo com determinado critério; plotados em um sistema de coordenadas cartesianas.
Os pares ordenados assim criados produzem o que se chama de gráfico da função. O conjunto dos valores x é chamado domínio da função, e o conjunto dos y é chamado imagem da função.
Nos pares ordenados, cada valor x é utilizado apenas uma vez.

Dom (f(x)) = [a; b] Im(f(x)) = [y_min; y_max]

Veja os gráficos de algumas funções de domínio real:

Função polinomial do primeiro grau

f(x) = ax
Retas, cujo crescimento depende do sinal do coeficiente a

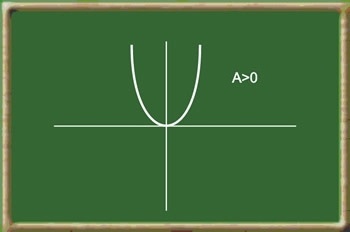
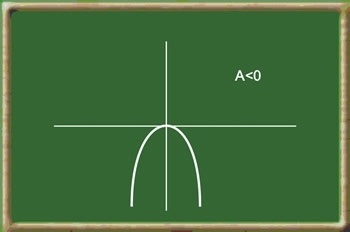
Função polinomial do segundo grau

f(x) = ax²

Parábolas, cuja concavidade depende do sinal do coeficiente a

Função polinomial do terceiro grau

f(x) = ax³

Função exponencial

f(x) = a^x
Curvas exponenciais, cujo crescimento depende do valor de a

Funções trigonométricas

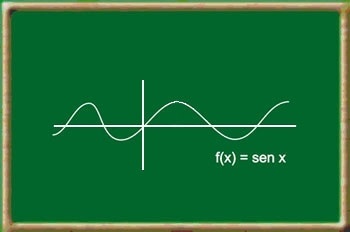Função modular

|x| = x se x  0
|x| = -x se x < 0

Funções cujos domínios são subconjuntos de r

7) f(x) = a/x

Para essas funções, Dom(f(x)) = R - {0}

f(x) = 

Função logarítmica

f(x) = log_b^X

http://educacao.uol.com.br/matematica/graficos-das-principais-funcoes-reconheca-as-curvas-mais-comuns.jhtm

_____________________________________________________________________________________________

FUNÇÃO CRESCENTE E FUNÇÃO DECRESCENTE DO 1º GRAU

As funções que são expressas pela lei de formação y = ax + b ou f(x) = ax + b, onde a e b pertencem ao conjunto dos números reais, com a ≠ 0, são consideradas funções do 1º grau. Esse tipo de função pode ser classificada de acordo com o valor do coeficiente a, se a > 0, a função é crescente, caso a < 0, a função se torna decrescente.

Vamos analisar as seguintes funções f(x) = 3x e f(x) = –3x, com domínio no conjunto dos números reais, na medida em que os valores de x aumentam.

Exemplo 1
f(x) = 3x

                                                             

                                               

Note que à medida que os valores de x aumentam, os valores de y ou f(x) também aumentam, nesse caso dizemos que a função é crescente e a taxa de variação da função é igual a 3.

Exemplo 2 f(x) = –3x
                                                             

                                                    

Nessa situação, à medida que os valores de x aumentam, os valores de y ou f(x) diminuem, então a função passa a ser decrescente e a taxa de variação tem valor igual a –3.

Outro fato importante para designar uma função é o seu gráfico, note que quando a função é crescente o ângulo formado entre a reta da função e o eixo x (horizontal) é agudo (< 90º) e na função decrescente o ângulo formado é obtuso (> 90º).

Então, a função é crescente no conjunto dos números reais (R), quando os valores de x1 e x2, sendo x1 < x2 resultar em f(x1) < f(x2). No caso da função decrescente no conjunto dos reais, teremos x1 < x2 resultando em f(x1) > f(x2). 

http://www.brasilescola.com/matematica/funcao-crescente-funcao-decrescente.htm

_________________________________________________________________________________

FUNÇÕES DO 2º GRAU

         Toda função estabelecida pela lei de formação f(x) = ax² + bx + c, com a, b e c números reais e a ≠ 0, é denominada função do 2º grau. Generalizando temos:

        As funções do 2º grau possuem diversas aplicações no cotidiano, principalmente em situações relacionadas à Física envolvendo movimento uniformemente variado, lançamento oblíquo, etc.; na Biologia, estudando o processo de fotossíntese das plantas; na Administração e Contabilidade relacionando as funções custo, receita e lucro; e na Engenharia Civil presente nas diversas construções.

          A representação geométrica de uma função do 2º grau é dada por uma parábola, que de acordo com o sinal do coeficiente a pode ter concavidade voltada para cima ou para baixo.

As raízes de uma função do 2º grau são os pontos onde a parábola intercepta o eixo x. Dada a função f(x) = ax² + bx + c, se f(x) = 0, obtemos uma equação do 2º grau, ax² + bx + c = 0, dependendo do valor do discriminante ? (delta), podemos ter as seguintes situações gráficas:

? > 0, a equação possui duas raízes reais e diferentes. A parábola intercepta o eixo x em dois pontos distintos.


? = 0, a equação possui apenas uma raiz real. A parábola intercepta o eixo x em um único ponto.

? < 0, a equação não possui raízes reais. A parábola não intercepta o eixo x.


http://www.brasilescola.com/matematica/funcao-segundo-grau.htm

_________________________________________________________________________________

INEQUAÇÕES DE 1º E 2º GRAUS

Uma inequação do 1° grau na incógnita x é qualquer expressão do 1° grau que pode ser escrita numa das seguintes formas:
ax + b > 0;
ax + b < 0;
ax + b ≥ 0;
ax + b ≤ 0.

Onde a, b são números reais com a ≠ 0.

Exemplos:

-2x + 7 > 0
x – 10 ≤ 0
2x + 5 ≤ 0
12 – x < 0

Resolvendo uma inequação de 1° grau

          Uma maneira simples de resolver uma equação do 1° grau é isolarmos a incógnita x em um dos membros da igualdade. Observe dois exemplos:

Exemplo1: Resolva a inequação -2x + 7  > 0.

Solução:
-2x > -7
Multiplicando por (-1)

2x < 7
x < 7/2

Portanto a solução da inequação é x  < 7/2.

Exemplo 2: Resolva a inequação 2x – 6 < 0.

Solução:
2x < 6
x < 6/2
x < 3

Portanto a solução da inequação e x < 3

          Pode-se resolver qualquer inequação do 1° grau por meio do estudo do sinal de uma função do 1° grau, com o seguinte procedimento:

1. Iguala-se a expressão ax + b a zero;

2. Localiza-se a raiz no eixo x;

3. Estuda-se o sinal conforme o caso.

Exemplo 1:
-2x + 7 > 0
-2x + 7 = 0
x = 7/2

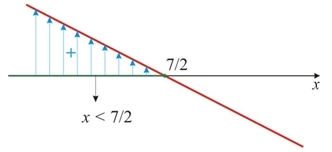
Exemplo 2:
2x – 6 < 0
2x – 6 = 0
x = 3

http://www.infoescola.com/matematica/inequacao-do-primeiro-grau/

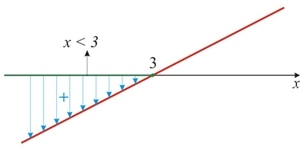
          As inequações do 2º grau são resolvidas utilizando o teorema de Bháskara. O resultado deve ser comparado ao sinal da inequação, com o objetivo de formular o conjunto solução.

Exemplo 1

Vamos resolver a inequação 3x² + 10x + 7 < 0.

S = {x E R / –7/3 < x < –1}


Exemplo 2

Determine a solução da inequação –2x² – x + 1 ≤ 0.

S = {x E R / x ≤ –1 ou x ≥ 1/2}



Exemplo 3

Determine a solução da inequação x² – 4x ≥ 0.

S = {x E R / x ≤ 0 ou x ≥ 4}


Exemplo 4

Calcule a solução da inequação x² – 6x + 9 > 0.

S = {x E R / x < 3 e x > 3}

http://www.brasilescola.com/matematica/inequacao-segundo-grau.htm

_________________________________________________________________________________

FUNÇÃO EXPONENCIAL

Toda relação de dependência, em que uma incógnita depende do valor da outra, é denominada função. A função denominada como exponencial possui essa relação de dependência e sua principal característica é que a parte variável representada por x se encontra no expoente. Observe:

y = 2 ^x
y = 3 ^{x + 4}y = 0,5 ^xy = 4 ^x
A lei de formação de uma função exponencial indica que a base elevada ao expoente x precisa ser maior que zero e diferente de um, conforme a seguinte notação:

f: R→R tal que y = a ^x, sendo que a > 0 e a ≠ 1.

Uma função pode ser representada através de um gráfico, e no caso da exponencial, temos duas situações: a > 0 e 0 < a < 1. Observe como os gráficos são constituídos respeitando as condições propostas:

Uma função exponencial é utilizada na representação de situações em que a taxa de variação é considerada grande, por exemplo, em rendimentos financeiros capitalizados por juros compostos, no decaimento radioativo de substâncias químicas, desenvolvimento de bactérias e micro-organismos, crescimento populacional entre outras situações. As funções exponenciais devem ser resolvidas utilizando, se necessário, as regras envolvendo potenciação.

Vamos apresentar alguns exemplos envolvendo o uso de funções exponenciais.

Exemplo 1(Unit-SE) Uma determinada máquina industrial se deprecia de tal forma que seu valor, t anos após a sua compra, é dado por v(t) = v₀ * 2 ^–0,2t, em que v₀ é uma constante real. Se, após 10 anos, a máquina estiver valendo R$ 12 000,00, determine o valor que ela foi comprada.
Temos que v(10) = 12 000, então:

v(10) = v0 * 2 ^–0,2*1012 000 = v0 * 2 ^–212 000 = v0 * 1/412 000 : 1/ 4 = v0
v0 = 12 000 * 4
v0 = 48 000

A máquina foi comprada pelo valor de R$ 48 000,00.

Exemplo 2
(EU-PI) Suponha que, em 2003, o PIB (Produto Interno Bruto) de um país seja de 500 bilhões de dólares. Se o PIB crescer 3% ao ano, de forma cumulativa, qual será o PIB do país em 2023, dado em bilhões de dólares? Use 1,03²⁰ = 1,80.

Temos a seguinte função exponencial

P(x) = P0 * (1 + i)^tP(x) = 500 * (1 + 0,03)²⁰
P(x) = 500 * 1,03²⁰
P(x) = 500 * 1,80
P(x) = 900

O PIB do país no ano de 2023 será igual a R$ 900 bilhões. 

http://www.brasilescola.com/matematica/funcao-exponencial-1.htm

___________________________________________________________________________________

FUNÇÃO LOGARÍTMICA

Toda função definida pela lei de formação f(x) = log_ax, com a ≠ 1 e a > 0 é denominada função logarítmica de base a. Nesse tipo de função o domínio é representado pelo conjunto dos números reais maiores que zero e o contradomínio, o conjunto dos reais.

Exemplos de funções logarítmicas:

f(x) = log₂x
f(x) = log₃x
f(x) = log_1/2x
f(x) = log₁₀x
f(x) = log_1/3x
f(x) = log₄x
f(x) = log₂(x – 1)
f(x) = log_0,5x 

Determinando o domínio da função logarítmica 

Dada a função f(x) = _{(x – 2)}(4 – x), temos as seguintes restrições:

1) 4 – x > 0 → – x > – 4 → x < 4
2) x – 2 > 0 → x > 2
3) x – 2 ≠ 1 → x ≠ 1+2 → x ≠ 3

Realizando a intersecção das restrições 1, 2 e 3, temos o seguinte resultado: 2 < x < 3 e 3 < x < 4.

Dessa forma, D = {x ? R / 2 < x < 3 e 3 < x < 4}

Gráfico de uma função logarítmica

Para a construção do gráfico da função logarítmica devemos estar atentos a duas situações:

? a > 1

? 0 < a < 1

Para a > 1, temos o gráfico da seguinte forma:
Função crescente

Para 0 < a < 1, temos o gráfico da seguinte forma:
Função decrescente


Características do gráfico da função logarítmica y = log_ax 

O gráfico está totalmente à direita do eixo y, pois ela é definida para x > 0.
Intersecta o eixo das abscissas no ponto (1,0), então a raiz da função é x = 1.
Note que y assume todos as soluções reais, por isso dizemos que a Im(imagem) = R.

Através dos estudos das funções logarítmicas, chegamos à conclusão de que ela é uma função inversa da exponencial. Observe o gráfico comparativo a seguir:

Podemos notar que (x,y) está no gráfico da função logarítmica se o seu inverso (y,x) está na função exponencial de mesma base.

http://www.brasilescola.com/matematica/funcao-logaritmica.htm

___________________________________________________________________________________