Exercícios complementares
1) Fatore os números:
a) 81 =
b) 144 =
2) Localize os números na reta numérica:
a) 9 b) -5 c) 0 d) -5
3) Antecessor, sucessor, simétrico, valor absoluto
a) Qual o antecessor de -3?
b) Qual o sucessor de 6?
c) Qual o número simétrico de -9?
d) Qual o valor absoluto de -15?
4) Elimine os parênteses:
a) ( -84 ) + ( +84 ) =
b) ( -6 ) + ( +6 ) =
c) ( +23 ) – ( +32 ) =
d) ( 16 ) + ( -16 ) =
5) Calcule o saldo:
Sra. Marisa
| |||
DATA
|
CRÉDITO
|
DÉBITO
|
SALDO
|
04/5
|
305,00
| ||
05/5
|
250,00
| ||
06/5
|
100,00
| ||
07/5
|
170,00
| ||
6) Coloque (P) para os números primos e © para os números compostos:
a) 11 ( )
b) 17 ( )
c) 25 ( )
d) 53 ( )
e) 91 ( )
7) Calcule o mmc de:
a) ( 2 , 3 ) =
b) ( 3 , 5 ) =
c) ( 2 , 3 , 5 ) =
d) ( 12 , 15 , 18 ) =
e) ( 5 , 8 , 9 ) =
8) Qual é o valor das expressões?:
a) ( -5 -2 ) + ( -5 +2 ) + ( 5 -2 )=
b) - ( 35 - 40 ) - { 5 - [ 10 + ( -7 -8 ) ] }=
_________________________________________________________________________________
Os princípios da balança, da adição e da multiplicação
Princípio aditivo
Princípio multiplicativo
_________________________________________________________________________________
Sistema de equação
Para encontrarmos numa equação de 1º grau com duas incógnitas, por exemplo,
4x + 3y = 0, os valores de x e de y é preciso relacionar essa equação com outra ou outras com as mesmas incógnitas. Essa relação é chamada de sistema.
Um sistema de equação de 1º grau com duas incógnitas é formado por: duas equações de 1º grau com duas incógnitas diferentes em cada equação. Veja um exemplo:
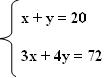
Para encontramos o par ordenado solução desse sistema é preciso utilizar dois métodos para a sua solução.
Esses dois métodos são: Substituição e Adição.
Método da substituição
Esse método consiste em escolher uma das duas equações, isolar uma das incógnitas e substituir na outra equação, veja como:
Dado o sistema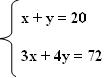 , enumeramos as equações.
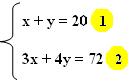
Escolhemos a equação 1 e isolamos o x:
x + y = 20
x = 20 – y
Agora na equação 2 substituímos o valor de x = 20 – y.
3x + 4 y = 72
3 (20 – y) + 4y = 72
60-3y + 4y = 72
-3y + 4y = 72 – 60
y = 12
Descobrimos o valor de y, para descobrir o valor de x basta substituir 12 na equação
x = 20 – y.
x = 20 – y
x = 20 – 12
x = 8
Portanto, a solução do sistema é S = (8, 12)
Método da adição
Esse método consiste em adicionar as duas equações de tal forma que a soma de uma das incógnitas seja zero. Para que isso aconteça será preciso que multipliquemos algumas vezes as duas equações ou apenas uma equação por números inteiros para que a soma de uma das incógnitas seja zero.
Dado o sistema:
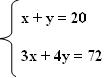
Para adicionarmos as duas equações e a soma de uma das incógnitas de zero, teremos que multiplicar a primeira equação por – 3.
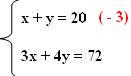
Agora, o sistema fica assim:
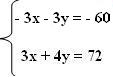
Adicionando as duas equações:
- 3x – 3y = - 60
+ 3x + 4y = 72 y = 12
Para descobrirmos o valor de x basta escolher uma das duas equações e substituir o valor de y encontrado:
x + y = 20
x + 12 = 20
x = 20 – 12
x = 8
Portanto, a solução desse sistema é: S = (8, 12).
Se resolver um sistema utilizando qualquer um dois métodos o valor da solução será sempre o mesmo.
_________________________________________________________________________________
4x + 3y = 0, os valores de x e de y é preciso relacionar essa equação com outra ou outras com as mesmas incógnitas. Essa relação é chamada de sistema.
Um sistema de equação de 1º grau com duas incógnitas é formado por: duas equações de 1º grau com duas incógnitas diferentes em cada equação. Veja um exemplo:
Para encontramos o par ordenado solução desse sistema é preciso utilizar dois métodos para a sua solução.
Esses dois métodos são: Substituição e Adição.
Método da substituição
Esse método consiste em escolher uma das duas equações, isolar uma das incógnitas e substituir na outra equação, veja como:
Dado o sistema
, enumeramos as equações. Escolhemos a equação 1 e isolamos o x:
x + y = 20
x = 20 – y
Agora na equação 2 substituímos o valor de x = 20 – y.
3x + 4 y = 72
3 (20 – y) + 4y = 72
60-3y + 4y = 72
-3y + 4y = 72 – 60
y = 12
Descobrimos o valor de y, para descobrir o valor de x basta substituir 12 na equação
x = 20 – y.
x = 20 – y
x = 20 – 12
x = 8
Portanto, a solução do sistema é S = (8, 12)
Método da adição
Esse método consiste em adicionar as duas equações de tal forma que a soma de uma das incógnitas seja zero. Para que isso aconteça será preciso que multipliquemos algumas vezes as duas equações ou apenas uma equação por números inteiros para que a soma de uma das incógnitas seja zero.
Dado o sistema:
Para adicionarmos as duas equações e a soma de uma das incógnitas de zero, teremos que multiplicar a primeira equação por – 3.
Agora, o sistema fica assim:
Adicionando as duas equações:
- 3x – 3y = - 60
+ 3x + 4y = 72 y = 12
Para descobrirmos o valor de x basta escolher uma das duas equações e substituir o valor de y encontrado:
x + y = 20
x + 12 = 20
x = 20 – 12
x = 8
Portanto, a solução desse sistema é: S = (8, 12).
Se resolver um sistema utilizando qualquer um dois métodos o valor da solução será sempre o mesmo.
_________________________________________________________________________________
Equação do 1º Grau
O fundamento das equações é alicerçado no próprio sentido etimológico da palavra equação. Esta palavra deriva de equatione, do latim, e significa equacionar, igualar. Baseado na definição etimológica da palavra equação entende-se que devemos procurar igualar o lado esquerdo ao lado direito da expressão. Quando isso acontece, diz-se que temos uma sentença verdadeira, uma igualdade, uma equação.
Toda expressão do tipo ax + b = 0, com a ≠ 0, representa uma equação de primeiro grau na incógnita x, onde a e b são os coeficientes da equação e x é a incógnita.
O coeficiente a deve ser diferente de zero ou então não teríamos a caracterização de equação, uma vez que o valor da incógnita também assumiria zero, neutralizando a nossa busca pelo elemento desconhecido. Além disso, não seria possível tornar a sentença verdadeira, fundamento primordial da equação. Acompanhem a expressão 0x + 9 = 0:
0x + 9 = 0, como 0 . x = 0 temos
0 + 9 = 0.
A sentença é falsa, pois 9 ≠ 0. Logo não temos uma equação (igualdade).
A caracterização de 1° grau se dá pelo fato da incógnita estar elevada ao expoente 1, vejam:
Por definição, todo número elevado à primeira potência resulta nele próprio. Sendo assim, omite-se o expoente 1, pois sua ausência, nesse tipo de situação, não desequilibra a sentença matemática.
Os princípios da balança, da adição e da multiplicação
Para compreendermos melhor a ideia de igualdade, necessário é que conheçamos o princípio da balança. Este princípio consiste em tornar os dois lados da igualdade equilibrados, com o mesmo “peso”. Basta para isso que imaginemos uma balança de dois pratos em perfeito estado de equilíbrio, ou seja, mesmo peso em ambos os pratos.
Dividamos a equação ax + b = 0 em duas partes. Ao lado esquerdo da igualdade chamaremos primeiro membro e ao lado direito chamaremos segundo membro.
O primeiro membro deverá sempre estar equilibrado em relação ao segundo. Quando adicionamos, subtraímos, multiplicamos ou dividimos um número qualquer no primeiro membro devemos também realizar a mesma operação no segundo membro.
Princípio aditivo
Através do princípio aditivo podemos adicionar ou subtrair os dois membros, simultaneamente, por um mesmo número que teremos uma nova igualdade.
Princípio multiplicativo
Este princípio consiste em multiplicar ou dividir os dois membros, simultaneamente, por um mesmo número. Ao final do processo teremos uma nova igualdade.
Regra prática
Existe um mecanismo prático para solucionar equações. Basta que sigamos algumas dicas:
- Reservaremos o primeiro membro (lado esquerdo da igualdade) somente para os valores desconhecidos (incógnitas);
- Ao segundo membro pertencerão os números não acompanhados da incógnita;
- Quando mudarmos um número ou uma incógnita de um membro para o outro inverteremos seu sinal.
Daniel é filho único e por isso tem uma boa mesada. O seu sonho era comprar uma skate e ser igual aos grandes skatistas brasileiros. Certo dia, ao entrar numa loja, ele encontrou uma ótima promoção: “Compre um skate e leve grátis uma bola de futebol”.
Sabe-se que o triplo do preço do skate com o preço da bola (R$ 50,00) dá um valor de R$ R$ 650,00. Ajude Daniel, encontre o valor unitário do skate.
Sabe-se que o triplo do preço do skate com o preço da bola (R$ 50,00) dá um valor de R$ R$ 650,00. Ajude Daniel, encontre o valor unitário do skate.
Chamemos de x o preço skate; 3x é o triplo do preço do skate; R$ 50,00 é preço da bola; R$650,00 é a soma de 3x comR$50,00.
Montando a equação
3x + 50 = 650
3x = 650 – 50
3x = 600
x = 600 : 3
x = 200
Portanto, R$ 200,00 é valor unitário do skate. Ainda mais, como foi informado na questão, a bola sairá gratuitamente gerando uma economia de R$ 50,00 caso ela fosse comprada separadamente.
Considerações Finais
Estudar as equações é importante para que sejam facilitadas as resoluções de problemas diários. Com o conhecimento dos conceitos sobre igualdades, podemos desenvolver nosso raciocínio lógico, solucionar problemas contendo valores desconhecidos, operar com os diversos grupos numéricos, passear pelos vários campos da matemática: funções, geometria plana e espacial, logaritmos e todos os ramos da matemática possíveis através do conhecimento das equações.
_________________________________________________________________________________
a) 3(x+y) ____ (R: )
b) 7(x-2y) ___ (R: )
c) 2x(x+y) ___ (R: )
d) 4x (a+b) ___ (R: )
e) 2x(x²-2x+5) _ (R: )
f) (x+5).(x+2) __ (R: )
g) (3x+2).(2x+1) __ (R: )
h) (x+7).(x-4) ____ (R: )
i) (3x+4).(2x-1) ___ (R: )
j) (x-4y).(x-y) ____ (R: )
k) (5x-2).(2x-1) ___ (R: )
l) (3x+1).(3x-1) ___ (R: )
m) (2x+5).(2x-5) __ (R: )
n) (6x²-4).(6x²+4) __ (R:
o) (3x²-4x-3).(x+1) __ (R: )
p) (x²-x-1).(x-3) _____ (R: )
q) (x-1).(x-2).(x-3) ____ (R: )
r) (x+2).(x-1).(x+3) ____ (R: )
s) (x³-2).(x³+8) _______ (R:
t) (x²+2).(x²+6) _______ (R:DIVISÃO DE UM POLINOMIO POR UM MONOMIO
Vamos efetuar as divisões:
a) (8x⁵ - 6x⁴) : (+2x) = 4x⁴ - 3x³
b) (15x³ - 4x²) : (-5x) = -3x² + 4x/5
Conclusão: Dividimos cada termo do polinômio pelo monômio.
EXERCÍCIOS
1) Efetue as divisões:
a) ( 12x² - 8x) : (+2x) =
b) (3y³ + 6y²) : (3y) =
c) ( 10x² + 6x) : (-2x) =
d) (4x³ - 9x) : (+3x) =
e) ( 15x³ - 10x²) : (5x²)
f) (30x² - 20xy) : (-10x)
g) (-18x² + 8x) : (+2x)
h) (6x²y – 4xy²) : (-2x)
2) Efetue as Divisões:
a) ( x³ + 2x² + x ) : (+x) =
b) (x² + x³ + x⁴) : (+x²) =
c) (3x⁴ - 6x³ + 10x²) : (-2x²) =
d) (x⁷ + x⁵ + x³) : (-x²) =
e) (3x²y – 18xy²) : (+3xy) =
f) (7x³y – 8x²y²) : (-2xy) =
g) (4x²y + 2xy – 6xy²) : (-2xy) =
h) (20x¹² - 16x⁸ - 8x⁵) : ( +4x⁴) =
i) (3xy⁴ + 9x²y – 12xy²) : (+3xy) =
_________________________________________________________________________________
_________________________________________________________________________________
Exercícios complementares
Monômios e Polinômios
Definição de monômio: Um monômio é uma expressão constituída por:
· um número ou uma letra (Exemplos: x; 2; z)
· ou um produto de letras ou de números com letras, em que as letras apenas têm expoentes naturais. (Exemplos:ab7; 3x2 )
Definição de polinômio: Um polinômio é a soma algébrica de dois ou mais monômios.
Exemplos:
· 5 - ab7 ; · x7 - 2x2+5
Atenção: Para qualquer monômio, podemos identificar o coeficiente, a parte literal e o seu grau (que se obtém somando os expoentes das letras).
Monômio
|
Coeficiente
|
Parte literal
|
Grau
|
-a/2
|
-1/2
|
a
|
1
|
2b
|
2
|
b
|
1
|
-10
|
-10
|
não tem
|
0
|
ab7
|
1
|
ab7
|
8 (grau de a + grau de b)
|
Monômios semelhantes: são monômios que têm a mesma parte literal.
Exemplos:-3b , 5b/3 , b (todos têm parte literal igual a b)
Monômios simétricos: são monômios que têm a mesma parte literal e os coeficientes simétricos.
Exemplos: -7xy3 , 7xy3
OPERAÇÕES COM POLINÔMIOS
ADIÇÃO DE POLINÔMIOS
EXEMPLO:
(3x²- 6x + 4) + (2x² + 4x – 7)=
=3x²-6x+4+2x²+4x-7=
=3x²+2x²-6x+4x+4-7=
=5x²-2x-3
EXERCÍCIOS
1) Efetue as seguintes adições de polinômios:
ADIÇÃO DE POLINÔMIOS
EXEMPLO:
(3x²- 6x + 4) + (2x² + 4x – 7)=
=3x²-6x+4+2x²+4x-7=
=3x²+2x²-6x+4x+4-7=
=5x²-2x-3
EXERCÍCIOS
1) Efetue as seguintes adições de polinômios:
a) (2x²-9x+2)+(3x²+7x-1) _______ (R: )
b) (5x²+5x-8)+(-2x²+3x-2) ______ (R: )
c) (3x-6y+4)+(4x+2y-2) ________ (R: )
d) (5x²-7x+2)+(2x²+7x-1) _______ (R: )
e) (4x+3y+1)+(6x-2y-9) _________ (R: )
f) (2x³+5x²+4x)+(2x³-3x²+x) _____ (R: )
g) (5x²-2ax+a²)+(-3x²+2ax-a²) ____ (R: )
h) (y²+3y-5)+(-3y+7-5y²) ________ (R: )
i) (x²-5x+3)+(-4x²-2x) __________ (R: )
j) (9x²-4x-3)+(3x²-10) __________ (R: )SUBTRAÇÃO DE POLINÔMIOS
EXEMPLOS
(5x²-4x+9)-(8x²-6x+3)=
=5x²-4x+9-8x²+6x-3=
=5x²-8x²-4x+6x+9-3=
=-3x²+2x+6
b) (5x²+5x-8)+(-2x²+3x-2) ______ (R: )
c) (3x-6y+4)+(4x+2y-2) ________ (R: )
d) (5x²-7x+2)+(2x²+7x-1) _______ (R: )
e) (4x+3y+1)+(6x-2y-9) _________ (R: )
f) (2x³+5x²+4x)+(2x³-3x²+x) _____ (R: )
g) (5x²-2ax+a²)+(-3x²+2ax-a²) ____ (R: )
h) (y²+3y-5)+(-3y+7-5y²) ________ (R: )
i) (x²-5x+3)+(-4x²-2x) __________ (R: )
j) (9x²-4x-3)+(3x²-10) __________ (R: )SUBTRAÇÃO DE POLINÔMIOS
EXEMPLOS
(5x²-4x+9)-(8x²-6x+3)=
=5x²-4x+9-8x²+6x-3=
=5x²-8x²-4x+6x+9-3=
=-3x²+2x+6
EXERCICIOS:
1) Efetue as seguintes subtrações:
a) (5x²-4x+7)-(3x²+7x-1) _____ (R: )
b) (6x²-6x+9)-(3x²+8x-2) _____ (R: )
c) (7x-4y+2)-(2x-2y+5) _______ (R: )
d) (4x-y-1)-(9x+y+3) _________ (R: )
e) (-2a²-3ª+6)-(-4a²-5ª+6) _____ ( R: )
f) (4x³-6x²+3x)-(7x³-6x²+8x) ___ (R: )
g) (x²-5x+3)-(4x²+6) _________ (R: )
h) (x²+2xy+y²)-(y²+x²+2xy) ____ (R: )
i) (7ab+4c-3a)-(5c+4a-10) ______ (R: )MULTIPLICAÇÃO DE POLINÔMIOSEXEMPLOS:
1) 4x(2x-3y ) =
=4x. 2x – 4x.3y
=8x² - 12xy
2) (3x + 5) . (x + 2)
= 3x(x+2) + 5(x + 2)=
=3x²+6x+5x+10
= 3x² + 11x + 10
EXERCICIOS
1) Calcule os produtos
a) (5x²-4x+7)-(3x²+7x-1) _____ (R: )
b) (6x²-6x+9)-(3x²+8x-2) _____ (R: )
c) (7x-4y+2)-(2x-2y+5) _______ (R: )
d) (4x-y-1)-(9x+y+3) _________ (R: )
e) (-2a²-3ª+6)-(-4a²-5ª+6) _____ ( R: )
f) (4x³-6x²+3x)-(7x³-6x²+8x) ___ (R: )
g) (x²-5x+3)-(4x²+6) _________ (R: )
h) (x²+2xy+y²)-(y²+x²+2xy) ____ (R: )
i) (7ab+4c-3a)-(5c+4a-10) ______ (R: )MULTIPLICAÇÃO DE POLINÔMIOSEXEMPLOS:
1) 4x(2x-3y ) =
=4x. 2x – 4x.3y
=8x² - 12xy
2) (3x + 5) . (x + 2)
= 3x(x+2) + 5(x + 2)=
=3x²+6x+5x+10
= 3x² + 11x + 10
EXERCICIOS
1) Calcule os produtos
b) 7(x-2y) ___ (R: )
c) 2x(x+y) ___ (R: )
d) 4x (a+b) ___ (R: )
e) 2x(x²-2x+5) _ (R: )
f) (x+5).(x+2) __ (R: )
g) (3x+2).(2x+1) __ (R: )
h) (x+7).(x-4) ____ (R: )
i) (3x+4).(2x-1) ___ (R: )
j) (x-4y).(x-y) ____ (R: )
k) (5x-2).(2x-1) ___ (R: )
l) (3x+1).(3x-1) ___ (R: )
m) (2x+5).(2x-5) __ (R: )
n) (6x²-4).(6x²+4) __ (R:
o) (3x²-4x-3).(x+1) __ (R: )
p) (x²-x-1).(x-3) _____ (R: )
q) (x-1).(x-2).(x-3) ____ (R: )
r) (x+2).(x-1).(x+3) ____ (R: )
s) (x³-2).(x³+8) _______ (R:
t) (x²+2).(x²+6) _______ (R:DIVISÃO DE UM POLINOMIO POR UM MONOMIO
Vamos efetuar as divisões:
a) (8x⁵ - 6x⁴) : (+2x) = 4x⁴ - 3x³
b) (15x³ - 4x²) : (-5x) = -3x² + 4x/5
Conclusão: Dividimos cada termo do polinômio pelo monômio.
EXERCÍCIOS
1) Efetue as divisões:
a) ( 12x² - 8x) : (+2x) =
b) (3y³ + 6y²) : (3y) =
c) ( 10x² + 6x) : (-2x) =
d) (4x³ - 9x) : (+3x) =
e) ( 15x³ - 10x²) : (5x²)
f) (30x² - 20xy) : (-10x)
g) (-18x² + 8x) : (+2x)
h) (6x²y – 4xy²) : (-2x)
2) Efetue as Divisões:
a) ( x³ + 2x² + x ) : (+x) =
b) (x² + x³ + x⁴) : (+x²) =
c) (3x⁴ - 6x³ + 10x²) : (-2x²) =
d) (x⁷ + x⁵ + x³) : (-x²) =
e) (3x²y – 18xy²) : (+3xy) =
f) (7x³y – 8x²y²) : (-2xy) =
g) (4x²y + 2xy – 6xy²) : (-2xy) =
h) (20x¹² - 16x⁸ - 8x⁵) : ( +4x⁴) =
i) (3xy⁴ + 9x²y – 12xy²) : (+3xy) =
_________________________________________________________________________________
Exercícios complementares 1º Bimestre
1) Fatore os números:
a) 81 =
b) 144 =
2) Localize os números na reta numérica:
a) 9 b) -5 c) 0 d) -5
3) Antecessor, sucessor, simétrico, valor absoluto
a) Qual o antecessor de -3?
b) Qual o sucessor de 6?
c) Qual o número simétrico de -9?
d) Qual o valor absoluto de -15?
4) Elimine os parênteses:
a) ( -84 ) + ( +84 ) =
b) ( -6 ) + ( +6 ) =
c) ( +23 ) – ( +32 ) =
d) ( 16 ) + ( -16 ) =
5) Calcule o saldo:
Sra. Marisa
| |||
DATA
|
CRÉDITO
|
DÉBITO
|
SALDO
|
04/5
|
305,00
| ||
05/5
|
250,00
| ||
06/5
|
100,00
| ||
07/5
|
170,00
| ||
6) Coloque (P) para os números primos e © para os números compostos:
a) 11 ( )
b) 17 ( )
c) 25 ( )
d) 53 ( )
e) 91 ( )
7) Calcule o mmc de:
a) ( 2 , 3 ) =
b) ( 3 , 5 ) =
c) ( 2 , 3 , 5 ) =
d) ( 12 , 15 , 18 ) =
e) ( 5 , 8 , 9 ) =
8) Qual é o valor das expressões?:
a) ( -5 -2 ) + ( -5 +2 ) + ( 5 -2 )=
b) - ( 35 - 40 ) - { 5 - [ 10 + ( -7 -8 ) ] }=
_________________________________________________________________________________
_________________________________________________________________________________
Nenhum comentário:
Postar um comentário